Z. Li and A. Chan Carusone
An Open-Source AMS Circuit Optimization Framework Based on Reinforcement Learning:
From Specifications to Layouts
in IEEE Access, vol. 12, pp. 150032-150045 (2024)
DOI: 10.1109/ACCESS.2024.3478832
Abstract: This paper presents a fully open-sourced AMS integrated circuit optimization framework based on reinforcement learning (RL). Specifically, given a certain circuit topology and target specifications, this framework optimizes the circuit in both schematic and post-layout phases. We propose using the heterogeneous graph neural network as the function approximator for RL. Optimization results suggest that it can achieve higher reward values with fewer iterations than the homogeneous graph neural networks. We demonstrate the applications of transfer learning (TL) in optimizing circuits in a different technology node. Furthermore, we show that by transferring the knowledge of schematic-level optimization, the trained RL agent can optimize the post-layout performance more efficiently than optimizing post-layout performance from scratch. To showcase the workflow of our approach, we extended our prior work to optimize latched comparators in the SKY130 and GF180MCU processes. Simulation results demonstrate that our framework can satisfy various target specifications and generate LVS/DRC clean circuit layouts.
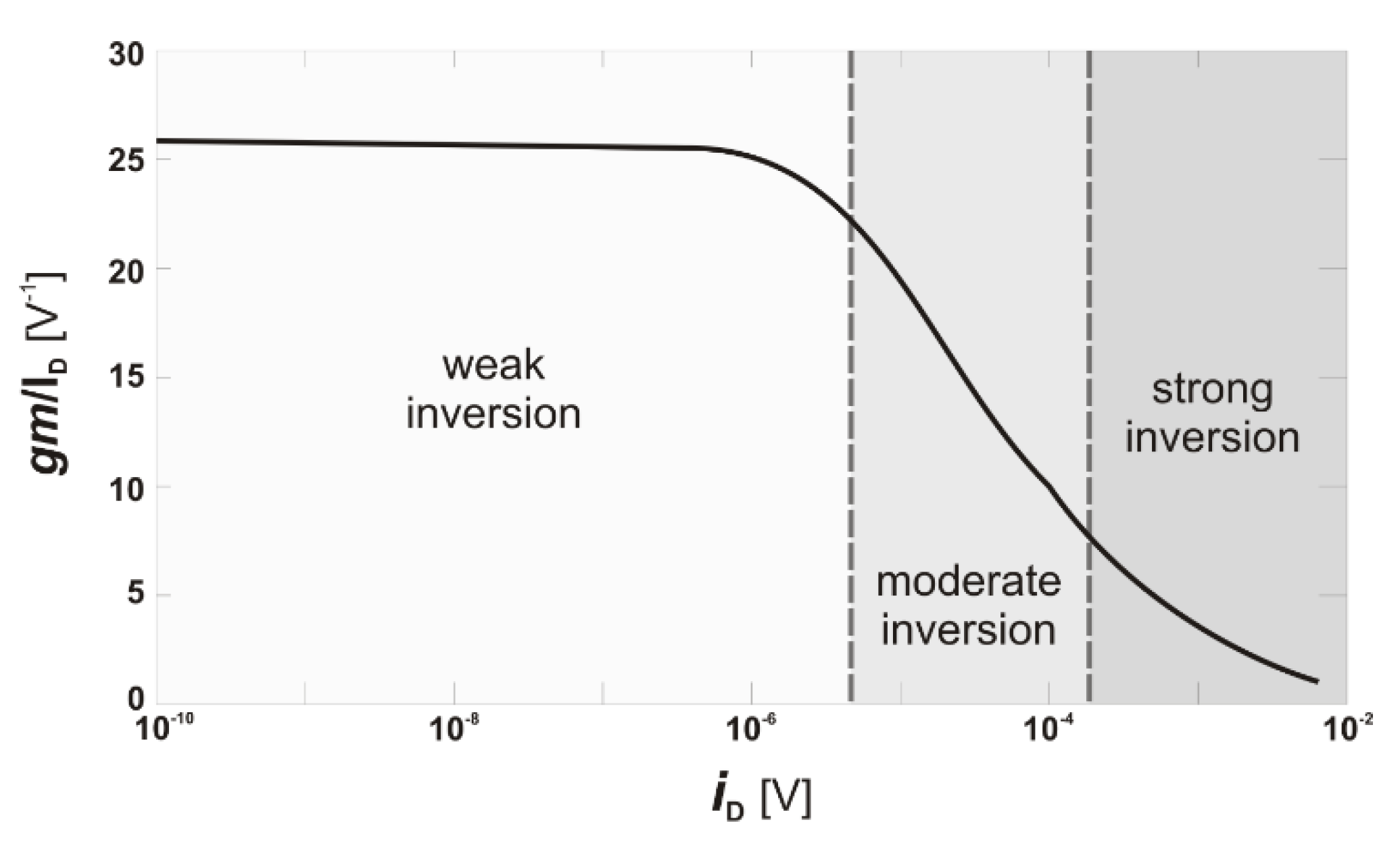
FIG: Proposed AMS IC optimizer overview.
The picture is adapted from [Z. Li and A. C. Carusone; 2023]
Acknowledgment: The authors would like to thank Dr. Hossein Shakiba from Huawei Technologies
for his valuable discussions throughout this project.
for his valuable discussions throughout this project.
[REF] Z. Li and A. C. Carusone, "Design and optimization of low-dropout voltage regulator using relational graph neural network and reinforcement learning in open-source SKY130 process," in Proc. IEEE/ACM Int. Conf. Comput. Aided Design (ICCAD), Oct. 2023, pp. 1–9.